Aus E=√E02+p2c2 kann geschlussfolgert werden, dass, wenn man die Gleichung zu √c2(m2c2+p2) umformt, dass dann zwei Kräfte in einem Teilchen agieren: die beschleunigende Kraft und eine Kraft senkrecht zur Bewegungsrichtung. Eine Kraft senkrecht zur Bewegung würde aber ein Teilchen in eine Drehbewegung um die eigene Achse versetzen, so dass diese eine Eigenrotation aufweisen würden. Auch Einstein hatte erkannt, dass zusätzlich zu der Bewegungsenergie noch eine zweite, intrinsische Energie den Teilchen innewohnt. Dass Teilchen eine Eigenrotation haben, sieht man schon alleine an ihrem Drehimpuls, laut Standardmodell rotieren Teilchen aber nicht in einem klassischen Sinne, was neuere Studien jedoch nicht bestätigen können. Der Term E0=m0c2 zeigt demnach die quantisierte Eigenrotationsenergie eines Teilchens an, die reelle, Eigenrotationsenergie ist z.B. bei Protonen allerdings sehr viel geringer, wie sich erst kürzlich zeigen ließ (1). Beim Proton gibt es zum einen die Rotationsenergie der Quarks mc2 und zudem die die Eigenrotationsenergie mc2/16. Die Masse, die bei mvr der Protonen, dem Drehimpuls, eingeht, berechnet sich aus der Gesamtrotationsenergie^2 - Eigenrotationsenergie^2.

E2=Em2+Er2=(E0+Er)2

An der Larmorfrequenz lässt sich dies bestätigen: 

f/B=e/2m(1+1/8)=42,57 kHz/T

Die fehlende Masse bei der alpha-Emission ist gleich der kinetischen Energie der Helium Teilchen, ihre Geschwindigkeit beträgt etwa ein Sechszehntel von c.  Dies lässt ebenfalls auf die Richtigkeit der oben gemachten Annahmen schließen: 

E02+Er2=E02+p2c2; (4mc2)2+(4mc2/16)2=(4mc2)2+16p2c2, v=√c2/16/16=c/16

"Drehen sich nun alle Teilchen mit Lichtgeschwindigkeit um sich selbst?"

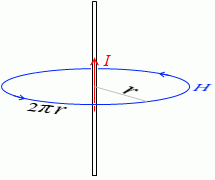
Drehen sich nun alle Teilchen mit Lichtgeschwindigkeit um sich selbst? Am Beispiel des Photons wird ersichtlich, dass dies nicht der Fall ist. Würde sich das Photon nicht um sich selbst drehen, sondern statt dessen eine Kreisbahn oder Ellipse beschreiben, dessen Radius genau der Wellenlänge des Photons dividiert durch 2π entspricht, dann wäre der quantisierte Rotationsenergiewert vollständig erfüllt. Die resultierende Bewegung eines Photons wäre dann eine Schraubenlinie oder eine andere daraus ableitbare Bewegungsform, was ja auch exakt so beobachtet wird. Im Unterschied zu Photonen weisen Neutrinos und Elektronen keine helikale Bewegungsform auf, ihre Eigenrotationsgeschwindigkeit dürfte sehr viel geringer als c sein, was sich analog zur Protonendrehgeschwindigkeit bestimmen ließe. Bei Neutrinos müssten andere Messeinrichtungen als die eines Beschleunigers gewählt werden, da sie nicht geladen sind. Die quantisierte Rotationsenergie und der Term E=m0c2 stimmt nur für kleinere Teilchen bei denen mcr<h/2π ist, für Nukleonen stimmt diese Gleichung allerdings nicht, da für diese Teilchen E0=m0c2/16 beträgt. Dies bedeutet aber, dass, wenn sich ein Teilchen in Ruhe befindet, seine Ruheenergie seiner Rotationsenergie entspricht.