Science Advance.
Science Advance. open online journal
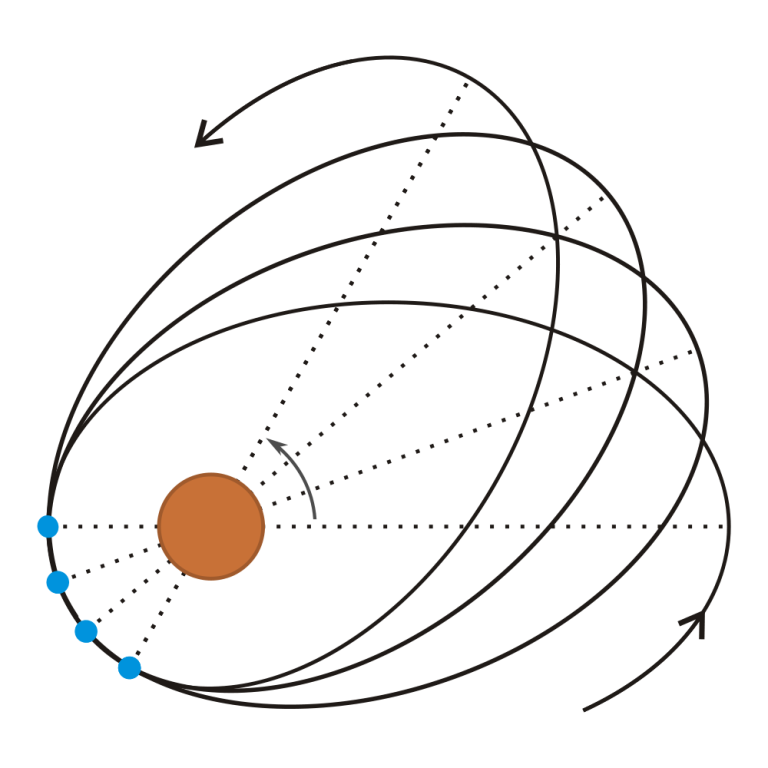
© Illustration twirl
Physics
Determination of the perihelion rotation using the barycentre method
Melissa B. Blau
University of Tübingen, Tübingen 72076, Germany
Published: 2023-05-22
https://doi.org/10.59208/sa-2023-05-22-6
Eprint: ViXra: 2284.4291340
Abstract:
Knowing the barycentre of the solar system and how far it is from the sun (up to twice the solar radius away), one can define fairly accurately how far the common barycentre of all planets (without the sun) is away, since the cumulative mass of the planets is well-known. From this, the orbital disturbance of planets close to the sun and also far from the sun can be reduced to a two-body problem. A very good approximation for the calculation of an orbital disturbance of a planet close to the sun using the barycentre method is φ = 2πbfa^2(1-e) per orbit, with b = 4.049*10^-28 [rad/m^2], a is the semimajor axis, f is a factor from the flattening of the planet and the reduced circumference of the orbit due to the eccentricity compared to 2πa and e is the eccentricity of the planet's orbit. The results are Mercury 574.14 arc seconds, Earth 1161.74", Saturn 2040.15" and Mars 1598.78" per century. Thus, the orbital perturbations using a planetary barycenter are fairly consistent with the measured data. Determining the difference to Newton's theory using general relativity calculations makes no sense as long as the theoretical numbers have not been determined with sufficient accuracy and as long as there are no differences between the measurement data and the theory when using the barycentric method. A computer simulation could help to exactly determine the perihelion rotation of the planets. The angle between the force effect and the orbital direction and the respective distance of the planet to the time-dependent variable planetary barycentre as well as the mean values from this would have to be determined frequently enough.
Cite this article
Blau M.B. Determination of the perihelion rotation using the barycentre method. Science Advance (2023). https://doi.org/10.59208/sa-2023-05-22-6
Science Advance.
Wir benötigen Ihre Zustimmung zum Laden der Übersetzungen
Wir nutzen einen Drittanbieter-Service, um den Inhalt der Website zu übersetzen, der möglicherweise Daten über Ihre Aktivitäten sammelt. Bitte überprüfen Sie die Details in der Datenschutzerklärung und akzeptieren Sie den Dienst, um die Übersetzungen zu sehen.